Hello.
I'm working on the construction of density radial profiles for gas, dark matter and star particles (and also their combination, i.e., dm + gas + stars). I followed the instructions here: dark matter and stellar binned masses.. My goal is to reproduce Figure 2. of Y. Wang et al.:
but, instead of obtaining a dm and total profiles density of order ~1e7 (it's clearly superior, but I'm using this for comparison), I got a result of order ~1e10 (c.f. fig. bellow)
I wish to know if I'm doing something wrong or missing some step. The script I constructed to generate this plot is shown below.
The units look ok, I suspect this is just a different volume normalization definition. Do I understand correctly, you are normalizing by the volume of a sphere (i.e. cumulative) instead of a shell (i.e. differential)? Usually you would make a radial density profile by diving by the volume of the spherical shell between a radius r0 and r1 for a given bin.
Pedro Ferreira
14 Jan '23
Yes, not using the volume of the spherical shell was my mistake. After correcting this part, I got the image below.
the difference in some points is due to the fact that the authors binned the radial interval in a logarithmic interval, while I binned it in a linear interval.
Hello.
I'm working on the construction of density radial profiles for gas, dark matter and star particles (and also their combination, i.e., dm + gas + stars). I followed the instructions here: dark matter and stellar binned masses.. My goal is to reproduce Figure 2. of Y. Wang et al.:
but, instead of obtaining a dm and total profiles density of order ~1e7 (it's clearly superior, but I'm using this for comparison), I got a result of order ~1e10 (c.f. fig. bellow)
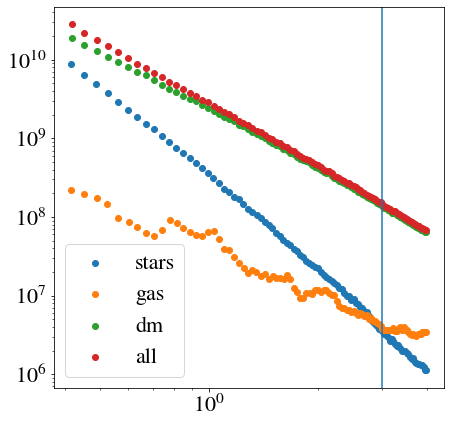
I wish to know if I'm doing something wrong or missing some step. The script I constructed to generate this plot is shown below.
At last, this is the subhalo used: (http://www.tng-project.org/api/TNG100-1/snapshots/z=0/subhalos/214452)
Thanks in advance.
The units look ok, I suspect this is just a different volume normalization definition. Do I understand correctly, you are normalizing by the volume of a sphere (i.e. cumulative) instead of a shell (i.e. differential)? Usually you would make a radial density profile by diving by the volume of the spherical shell between a radius
r0andr1for a given bin.Yes, not using the volume of the spherical shell was my mistake. After correcting this part, I got the image below.
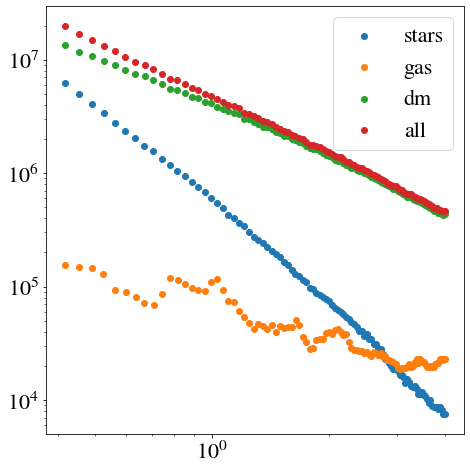
the difference in some points is due to the fact that the authors binned the radial interval in a logarithmic interval, while I binned it in a linear interval.